What's Big O mean

Do you know how long it will take to run this little code?

// 'a' is an array
for (let i = 0; i < a.length; i++ ){
  if (a[i] == 'lucy'){
    console.log('yeah, a lucky day ')
  }
}

It receives an array as args and print lucky day for each lucy element in this array. let’s see how many steps it runs:

Assume that a.length = N, then

#1 Init i=0, run only once (1 time)

#2 Need to check each element to see if it is our lucy (N times)

#3 Depends on the elements in array, it runs only when the element is ’lucy’ (0 time ~ N times)

#4 Check if we have checked all elements (N-1 times)

#5 Go to check the next element (N-1 times)

#6 Exit function

The total max number of those steps it runs is:

$1 + N + MAX(0, N) + (N-1) + (N-1)$ => $ 4N - 1$

That means giving an array which contains N elements to hello function, it runs 4N - 1 steps at most. But we still don’t know how long it will take to run those 4N -1 steps.

One of the reasons is that we don’t know how many machine code steps this function will be converted to by the compiler（Maybe one if statement to 2 machine code statements, and one = statement to 1 machine code statement, cannot exactly know because we don’t even know which compiler will be used). The second reason is similar to the first one: cannot exactly know the time spends on each machine code statement because we don’t know which CPU will be used.

Obviously, we will never know the exact time just with the code, all we can do is that ignore the compiler and CPU then assume the function of time complexity $T(n)$, for hello function $T(n)=4n - 1$.

To be more abstract and simpler, there are 2 rules can be applied to simplify $T(n)$:

• Drop the lower order terms
• Ignore all constants

This is what we call big o: $O(n)$

e.g.

• $T(n)=4n - 1$ => $O(n)=n$
• $T(n)=4n^3 + n^2 + 10000$ => $O(n)=n^3$

Drop the lower order terms because it is usually insignificant compared to high-order items. See the diagram below then you will know what I mean:

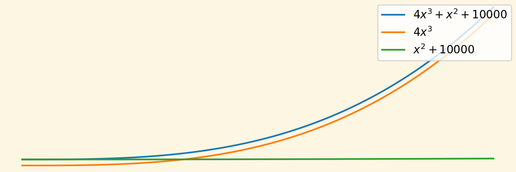
About the constants in $T(n)$ , we ignore them because they are releted to some uncertain factors as we mentioned before (CPU, compiler and so on), running a function on a supercomputer is a thousand times faster than running it on a Raspberry.